A Demo on Hidden Markov Models

_{The code for this demo is available here}

Hello all,

Today I bring you some of the latests interesting projects I have been dealing with. In one of the courses I’m currently attending “Estimation and Classification”, we were asked to solve the following toy problem:

Consider a robot located inside a small sized finite 2D environment, limited by boundaries and populated with obstacles. Assume this environment to be fully representable with a discretized grid, where each grid node may be occupied by an obstacle. The robot itself can only occupy an obstacle-free node at each time instant. The robot is equipped with a sensing device that can detect adjacent obstacles in its neighborhood, also providing their relative location. The motion model of the robot allows it to travel to adjacent nodes in each iteration, as long as it is within the boundaries and is not occupied by an obstacle. Given the conditions described and the robot’s access to the map of the environment, determine the probability of the robot being in a specific node, considering all observations made.

It can be shown that this problem verifies all the necessary conditions to be considered a Hidden Markov Model (HMM) and that it can be solved resorting to Baum’s Forward algorithm. I will spare you from all the theoretical formulation because I’m only interested in showing the results.

The following work was conducted with the help of Gonçalo Cruz from the Portuguese Air Force Academy.

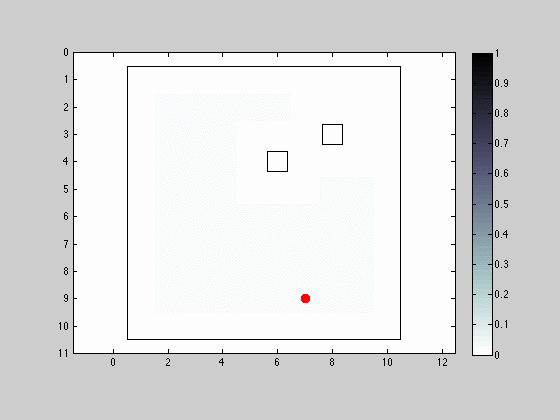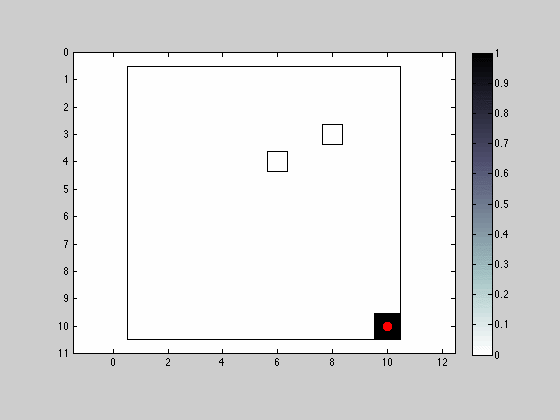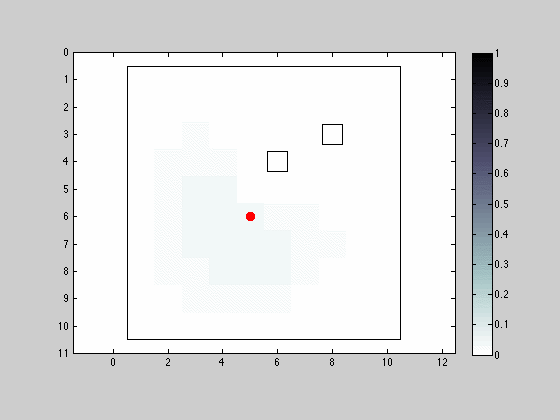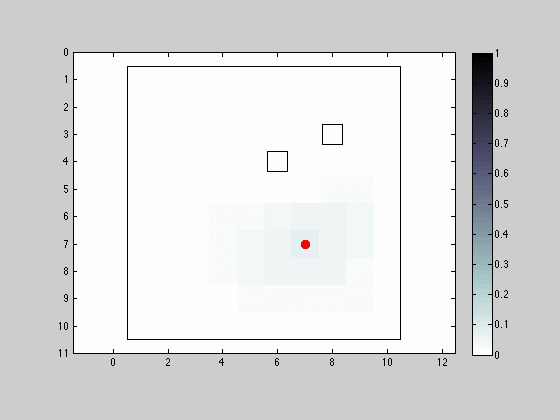
Movement and Sensing in the 4 Neighborhood

The first simulation addresses a situation where the robot is force move with each iteration, choosing its destination from the vicinity nodes in the 4 neighborhood. The sensor is able to detect obstacles in its 4 neighborhood also.

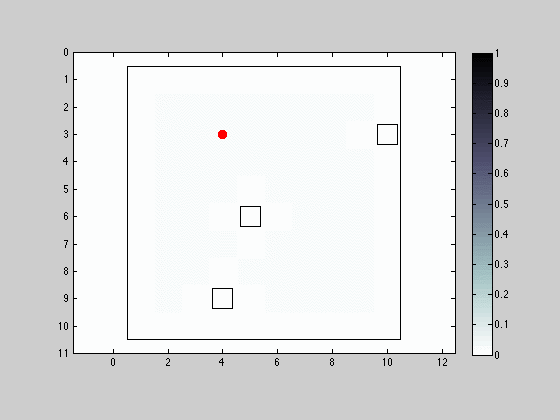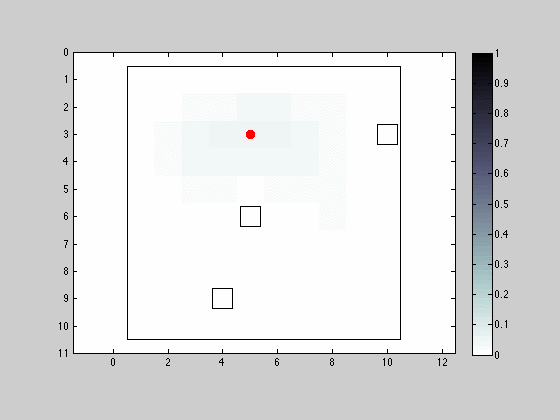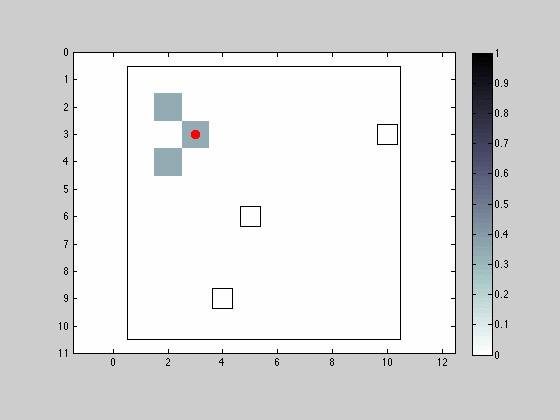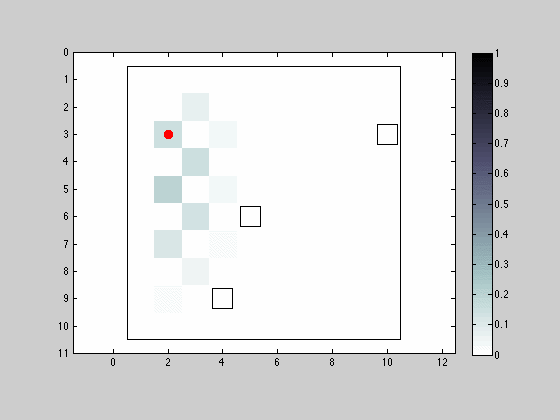
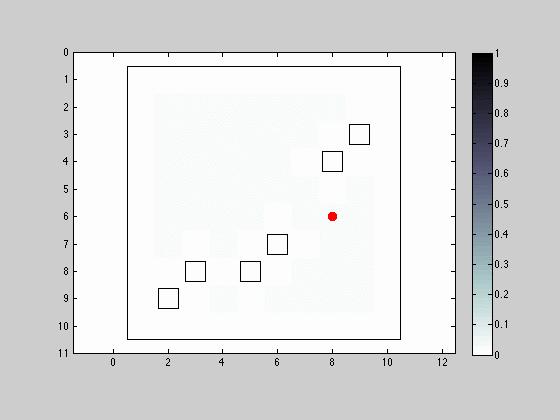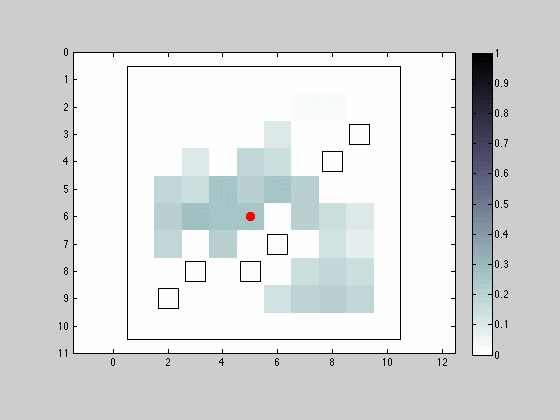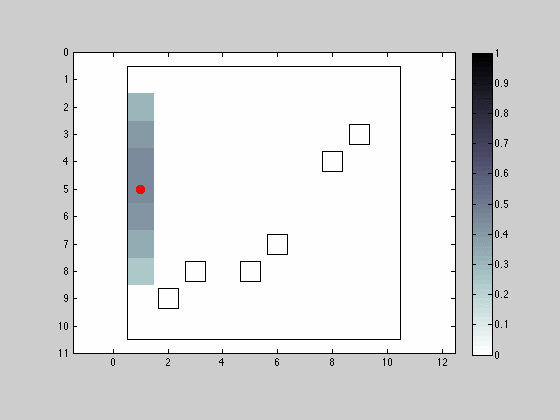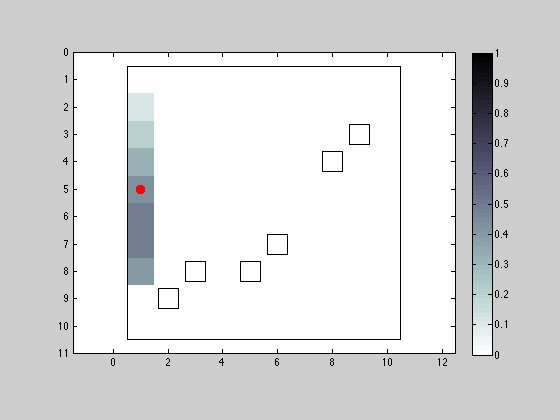
The red dot represents the robot’s actual position and the hollow squares denote obstacles. The initial distribution is uniform for all grid nodes. There are a few interesting remarks to point out: when the robot can sense an obstacle to its right, it is intuitive to see that all visible eligible locations for the robot after filtering have an obstacle to the right; if the robot spends too much time without sensing an obstacle, the distribution of the probabilities spread out, eventually concentrating more on the interior regions of obstacle free areas; the grid/intermittent alike structure that is imposed on the probability distribution after the robot’s location is accurately determined, resultant from the forced movement constraint at each iteration.

Movement and Sensing in the 4 Neighborhood Allowing Position Maintenance

This simulation resembles the previous one in almost its entirety with the modification that now the robot can remain in the same location between iterations. The sensing capabilities remain similar.

The grid/intermittent pattern is now lost because robot is able to remain in the same position.

Movement and Sensing in the 8 Neighborhood Allowing Position Maintenance

In this third simulation we modify the moving and sensing capabilities of the robot to now operate the 8 neighborhood.

The effects of having improved sensing capabilities have a noticeable greater effect in uncertainty reduction in the presence of obstacles.

Movement and Sensing in the 8 Neighborhood Allowing Position Maintenance and Considering Observation Error

For this last simulation, a modification was made to the previous one, so that the obstacle detection sensor would sometimes output an erroneous observation. The sensor reproduces a behavior where it will actually output incorrect measurements based on some assigned probabilities. For the example displayed bellow the sensor only outputs an accurate measurement 50% of times

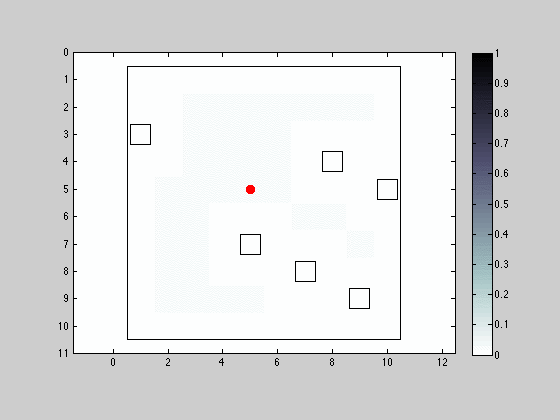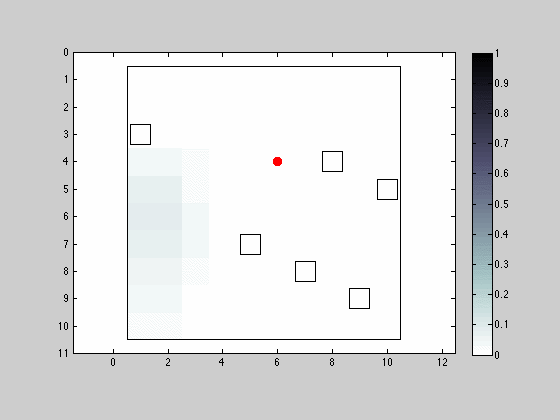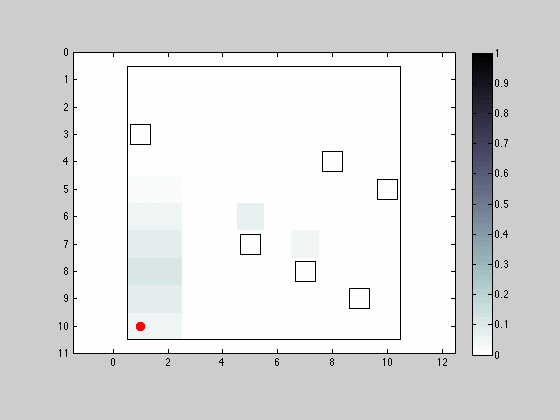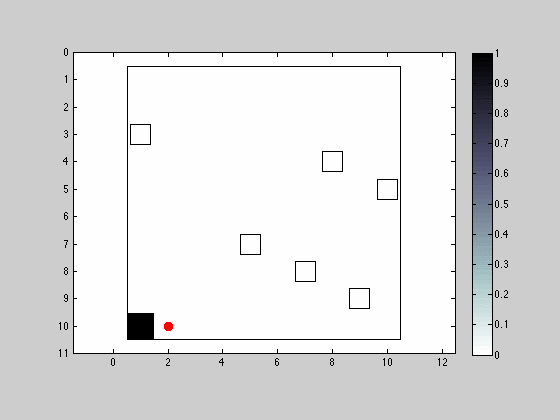
The effect of having an imperfect sensor manifests itself when filtering stages occur based on spurious observations, shifting the most likely robot location to entire different regions of the map. Although barely visible (if at all), the robot can never reach a situation where he is fully certain of the robots location.

Hope you enjoyed it,

Sérgio